Sudoku Strategies

There are a number of different strategies to solve a Sudoku. In this article I will present some of the simpler variety. If you are not familiar with the number puzzle Sudoku, you can have a look at the Rules of Sudoku before you start reading about Sudoku solving methods.

For a much more detailed explanation of easy, advanced and difficult solving strategies (as well as many examples and exercises), you can also have a look at my Book on Sudoku Strategies.

Basic Sudoku solving techniques

The simplest case is when only one field is left empty in a row, column or block. In such a case, you only have to look which number is still missing in this row/column/block and enter it into the free field. The following image gives an example of thiy type:

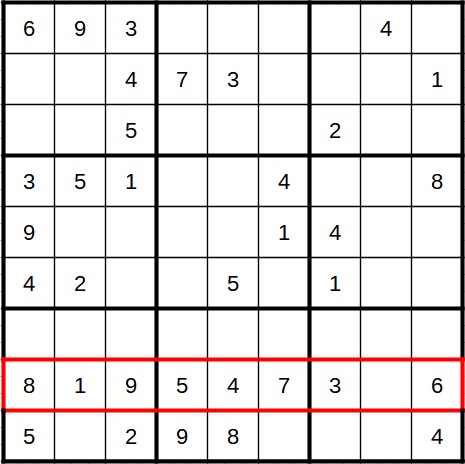
As we can see, in the eighth and penultimate row, eight of nine fields are already occupied. The only missing digit is the 2. So we enter it in the free field.

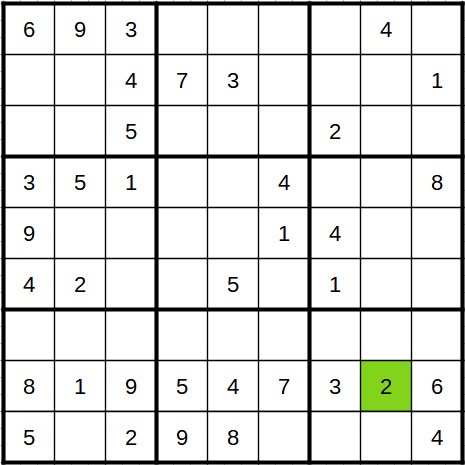
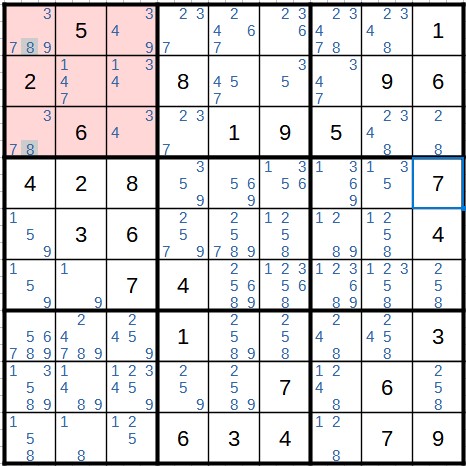
Of course, it's not always as simple as the example above. If more than one field is empty in a row/column/block, you have to try to find out if there is only one possible candidate in a field by scanning the other fields. In the following Sudoku puzzle, we look at the block on the bottom right.

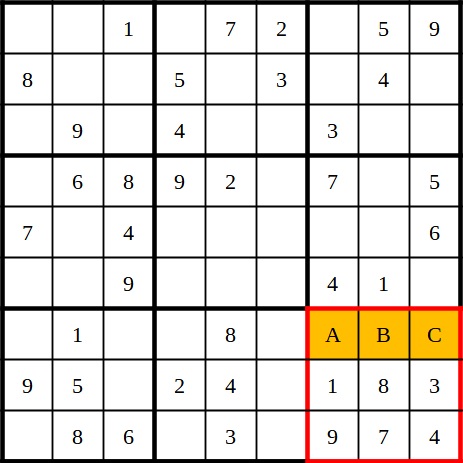
The numbers 2, 5, and 6 are still missing in this block, so we look at columns 7, 8, and 9 because they are adjacent to this block and directly affect the missing cells. In the last column, the 5 and the 6 are already present. Therefore, only the 2 is possible in cell C. For A and B, the 5 and 6 remain. But in column 8 there is already the 5, so for cell B only the 6 remains. Thus, the 5 is the only remaining candidate for cell A.

Solving Sudoku by simple scanning methods

In the same example, we can now look at the eighth column. There, only two digits are missing: 6 and 7. However, the 6 is already present in the lower left block, which is why we can enter the 7 in the third cell of the eighth column. For the last remaining cell, only the 6 remains.

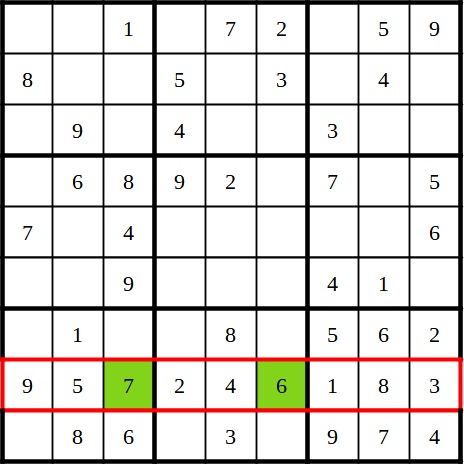
Afterwards, you can proceed exactly the same way and solve the Sudoku this way.

In the following example there is only one possibility in the cell marked by the question mark.

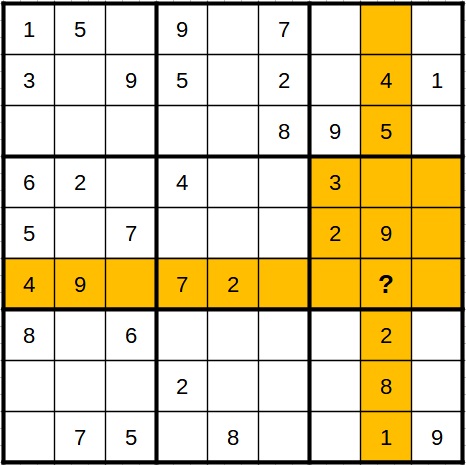
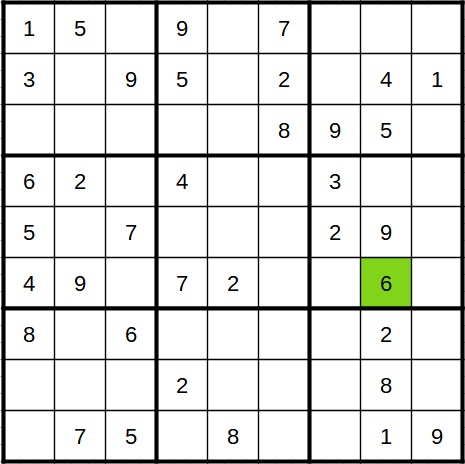
In the same column, the 1, 2, 4, 5, 8 and 9 are already there and cannot occur again. In the same block there is also already the 3 and in the same line the 7. So only the 6 is missing, which we can enter for the question mark.

Advanced Sudoku strategies

The above scanning techniques can be used to solve many Sudokus that can be found in daily newspapers or magazines or on the Internet. At least if they have an addition such as 'easy' or 'for beginners'. But sometimes you are stuck with a Sudoku puzzle using these basic techniques. In this case, the possible candidates are often written in all empty cells (small or in pencil so that they can be erased later).This may look like the following image:

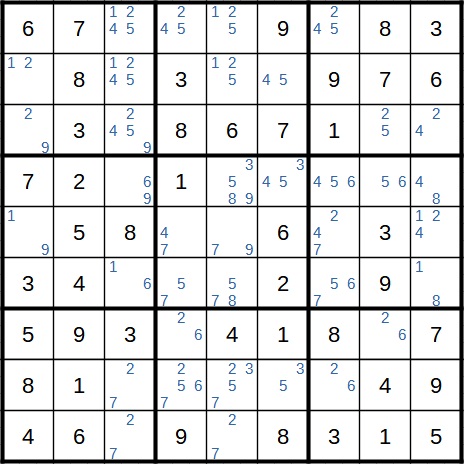
We can see here that only the candidates that are really suitable are entered for each cell. This becomes clear in the ninth and last row. Only two digits are missing here, the 2 and the 7. So we only write the 2 and the 7 as candidates in these two cells.

These candidates are now helping us to find the solution. Other solution methods are based on this candidate notation. In the following, I will therefore present a few advanced Sudoku strategies.

Naked Pair in Sudoku

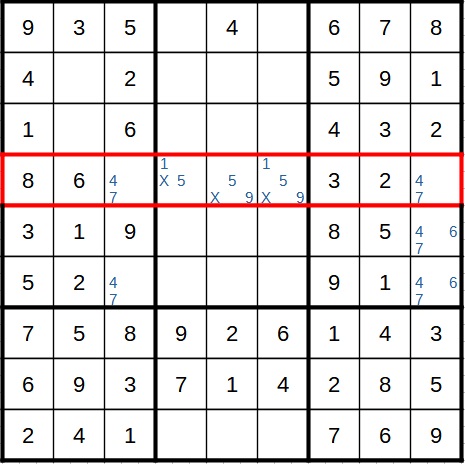
A naked pair exists in Sudoku when there are two cells in which only two digits are possible candidates (the same two digits in both cells). As in the following image in the row that is marked in red:

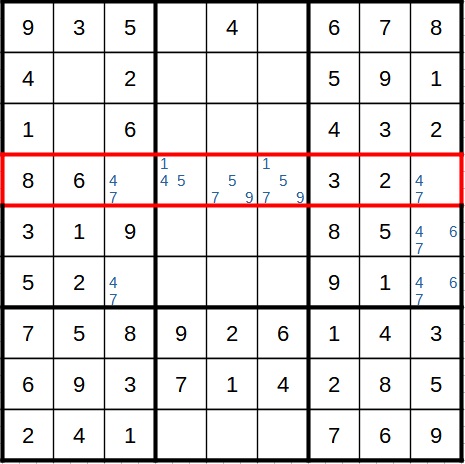
In this row, we have two cells in which only the 4 and the 7 appear as candidates. What does this mean for us? This means that one of these two cells contains the 4 and the other contains the 7. We don't yet know the exact order in which they appear, but we know from the Sudoku rules that the 4 and the 7 cannot be in any other position in this row. 4 and 7 are referred to as a 'naked pair' because there were no other candidates in these cells. They were immediately visible and therefore virtually naked.

Based on this logic, we can remove the 4 and the 7 from all other cells in this row as candidates. This becomes clear in the next picture:

Naked Triple

The naked triple is based on the naked pair and is therefore easy to explain. Instead of two cells with two candidates, here we have three cells and three candidates. The difference is that not all three candidates have to occur in each of the three cells. Let's take a look at the next example:

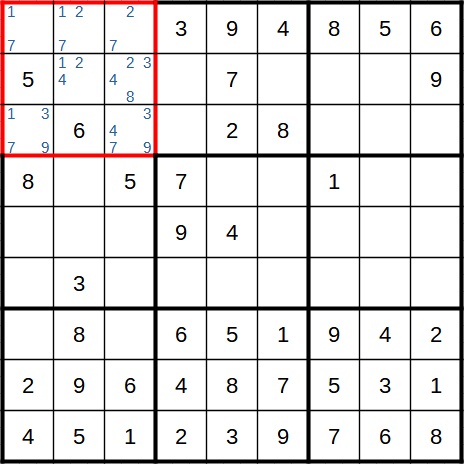
In the block that is marked in red, we have three cells that only contain the candidates 1, 2 and 7. It does not matter that not every cell contains all three candidates. The only important thing is that only these three fields contain the three digits (in whatever order). For this reason, we can again remove the 1, the 2 and the 7 from other cells in this block, as in the next picture:

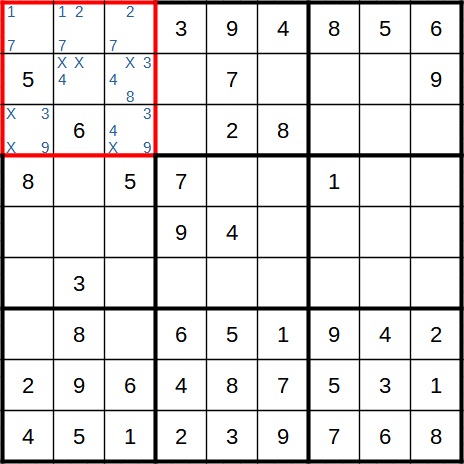
We can now apply the same principle to a quadruplet of digits. I hope the logic behind this Sudoku solving method has become clear.

Hidden Pair and Hidden Triple in Sudoku

After the naked pair and the next triple, th the hidden there is also a method called hidden pair or hidden triple. Here we proceed in a similar way by again searching for a pair or triple within a row, a column or a block.

The difference here is that there are other candidates in the cells. The pairs or triples are therefore hidden, so to speak. Let's take a look at an example of the hidden pair. It's about the block at the bottom left.

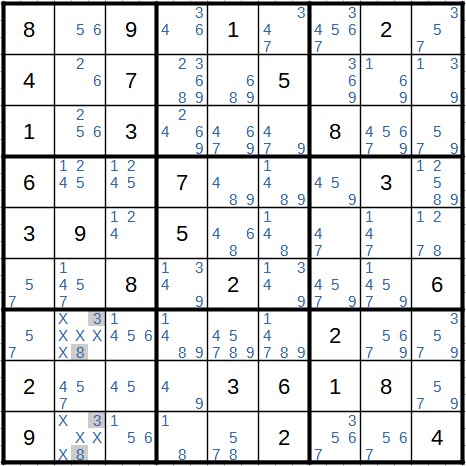
There are only two cells in this block, which can contain the 3 and the 8. However, every block in Sudoku must contain every digit from 1 to 9. So one of these two cells contains the 3 and the other the 8. We can therefore remove all other candidates from these fields.

Finally, an example of the hidden triple. In the eighth row, there are only three cells in which the candidates 1, 3 and 9 can occur. We can therefore remove all other candidates from these three cells.

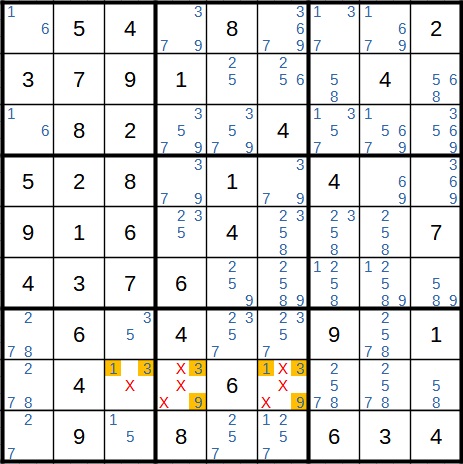
Intersection Removal as a Sudoku strategy

For intersection removal, we also need the candidates in the empty cells. This Sudoku technique is difficult to explain in words, which is why we will look at three examples below. We can distinguish between three cases here:

1. If there is a row in which a candidate is restricted to one block, this candidate can be removed from all other positions in this block
2. If there is a column in which a candidate is restricted to one block, this candidate can be removed from all other positions in this block
3. If there is a block in which a candidate is restricted to one row/column, this candidate can be removed from all other positions in this row/column

Let's start with an example of the first case:

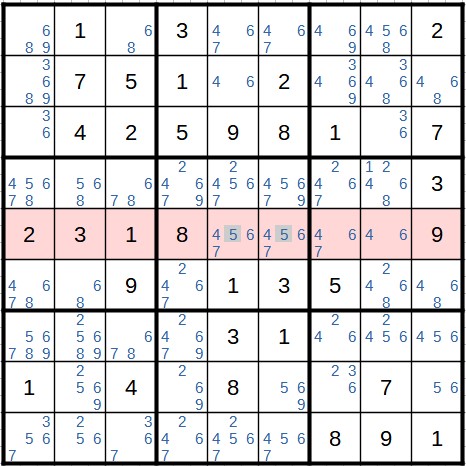
In the fifth row, the candidate 5 only appears in the block in the middle. However, as each row must contain every candidate, including the 5, the 5 is inevitably in one of these two cells. It cannot appear again in this block. We can therefore remove it from other cells in the block.

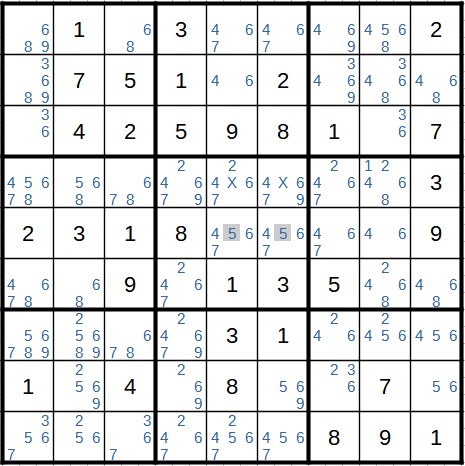
The next example shows the second case. Here, the 1 only appears in the block in the middle of the seventh column. It is therefore also in one of these two cells. We can remove the 1 from two other cells in this block.

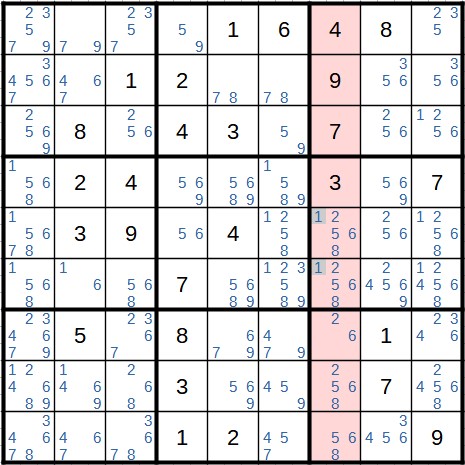
And last but not least, an example of the third case. Here, candidate 8 is restricted to the first column in the top left block. We therefore remove the 8 from all other cells in this column.

For more advanced and difficult Sudoku strategies you can check the great site sudokuwiki.org.

If you speak German, you can also have a look at sudoku-hilfe.de and the page Sudoku-Strategien.